I have to start by correcting an omission: last week I talked about 2024 and square pyramidal numbers, and I did not mention that 2024 is also a pyramidal number, although not square but triangular. Fortunately, my kind readers are usually on point: Javier Tamames reminded me that 2024 is a tetrahedral number (as triangular pyramidal numbers are also called) and Ignacio Larrosa sent an eloquent visualization in the shape of a triangular pyramid of stacked spheres, whose 22 levels add up to 2024.
A pyramid whose base is a triangle is a tetrahedron, and therefore triangular pyramidal numbers are also called tetrahedral. If in the visualization of the stacking of spheres we add those of each level, starting from the top, we obtain the sequence of the tetrahedral numbers (corresponding to the number of spheres of the tetrahedra of 1, 2, 3, 4… spheres on each side): 1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364…
The successive levels of the pyramid form, in turn, the sequence of triangular numbers (displayable as equilateral triangles of spheres):
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78…
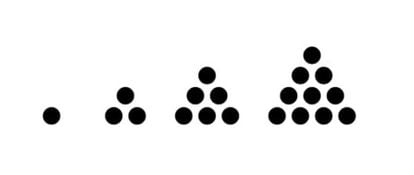
And, therefore, the nth tetrahedral number (Tn) is the sum of the first n triangular numbers:
T1 = 1
T2 = 1 + 3 = 4
T3 = 1 + 3 + 6 = 10
T4 = 1 + 3 + 6 + 10 = 20
T5 = 1 + 3 + 6 + 10 + 15 = 35
…
T22 = 1 +3 + 6 + 10 + 15 + 21 + 28… + 210 + 231 + 243 = 2024
Can you find a formula that allows you to determine that the twenty-second tetrahedral number is 2024 without having to perform the previous long addition?
A little more difficult: Comparing the two lists above, we see a match: 10, which means that the third tetrahedral number is equal to the fourth triangular number. Can you find more numbers that are both triangular and tetrahedral?
Even more difficult: among the first tetrahedral numbers there are two that are perfect squares: 1 and 4. Can you find any more or prove that they do not exist?
Zener's letters
In addition to being a teacher of scientific popularizers, Martin Gardner was a relentless unmasker of fallacies, pseudosciences and various paranormalities, and sometimes ironically used the arguments of magufos, or their instruments, as raw material for his mathematical hobbies.
In an interesting article brought up by Manuel Amorós, Gardner starts from Zener's letters (today fallen into well-deserved oblivion, but once very popular), used to evaluate supposed telepathic abilities, to pose an interesting problem of covering, which has raised a lively debate among the readers (see comments from last week).
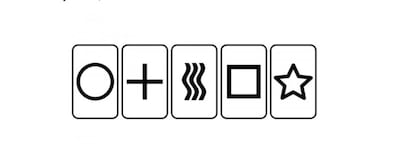
Which of these five symbols can be drawn álef 1 times on paper, assuming that they are drawn with ideal lines, without thickness, and that they do not overlap or intersect each other? The symbols can be of different sizes, but they must be geometrically similar. Let us remember that alef 1 is the non-countable infinity of real numbers.
It turns out that all but one of the symbols can be drawn aleph 1 times. Can you tell which one it is and why? A double question with two levels of difficulty, because it is relatively easy to demonstrate that the four drawable symbols countless (literally) times are, thus identifying, by elimination, the one that is not. But demonstrating why it is not so is no longer so simple, and Gardner himself limits himself to outlining a solution that is not entirely clear.
You can follow SUBJECT in Facebook, x and instagramor sign up here to receive our weekly newsletter.
#tetrahedral #numbers
