In mathematics, we often start with a simple question, which leads us down unexpected paths. For example, how many times is it possible to knot a rope on itself? In the real world, various physical constraints determine the answer: the length of the string, its elastic capacity and thickness… If we strip the question of all these physical constraints we are left with a mathematical question.
A mathematical knot is an elastic curve that is entangled in space and can be deformed by manipulating its parts without breaking them. Mathematical knots have their ends glued together, like the line that draws a circle. That is the simplest knot, the trivial knot; but he’s not the only one.
The diversity of these mathematical objects is infinite and one of the tasks of knot theory -which is an area of topology- is to describe it. To do this, it is necessary to determine when two knots are the same: they will be when it is possible to deform one into the other, without breaking it. Hopefully, this process ends at some point, when they are the same, but conversely, if they are not, we can spend a lot of time without reaching any conclusion.
To save us this path, the theory of knots is responsible for identifying mathematical properties that can be verified more easily. Of these, the simplest is to count how many times the curve is crossed by drawing it on a sheet of paper, indicating which part crosses above and which part below, at each crossing.
However, the same node can have many different diagrams; not only according to the point of view from which it is drawn, but also, there could be some crosses that would disappear simply by twisting, a little, some part of the knot.
The minimum number of crossings that can be achieved in a knot diagram allows one to tell if two knots are different; for example, if one has three and the other four. And it also allows you to organize the knots in a large catalog, starting with the simplest: the circle, or trivial knot, which can be drawn without any crossing.
All knots that can be drawn with one or two crosses can be manipulated in such a way that they are identical to a circle. There is only one knot with three crossings and it is known as the “cloverleaf knot”. The “eight knot” is the only one that can be drawn with four crosses, but from there, the diversity grows rapidly. The catalog of knots with up to ten crossings has 250 different knots, and with up to 19 the number amounts to more than 300 million.
A wild knot has an infinite number of crosses and answers the question with which we started this text. To imagine it, we can use a recipe that, although infinite, is relatively simple. An important ingredient in the recipe is spherical mirrors, which show, on their surface, the reflected image of the entire space, as if it were inside the sphere. This mirror deforms most figures: straight lines appear curved and it is inevitable to think of a fish when looking at our reflected face. The only figure that does not change when reflected, except for its size, is the figure of any other sphere.
The key to the recipe is in this property, because that other sphere could also be made of a mirror and, in that case, if we look carefully, we could observe, in the reflection of that sphere, the reflected image of the initial sphere …a tongue twister. To build a wild knot, one starts from a knot from the catalogue, any one works except the trivial knot, and a few spherical mirrors are also needed, which can be of different sizes. Then, the spheres are strung, one by one, on an imaginary rope, ensuring that they are tight enough so that the consecutive spheres touch at a point, to form a necklace.
Next, the necklace is tied according to the diagram of the chosen knot and closed at its ends, ensuring that the spheres at the ends also touch. In each of the spheres of the necklace a copy of the rest of the necklace is reflected and these pieces of necklace are connected, in consecutive spheres, forming a new necklace, made of smaller spheres. This new necklace is more intricate than the previous one, because in each piece you can see the shape of the knot repeated in each sphere. In addition, since it is also made of reflective spheres, we can repeat the previous step in this new necklace and so on, and again… ad infinitum.
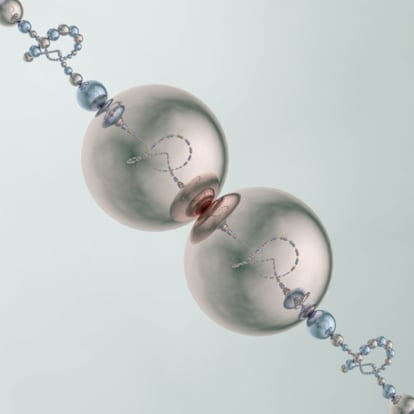
The wild knot has endless details getting smaller and smaller. And, thanks to mathematics, we know that inside all these necklaces there is only one thin curve without ends, infinitely knotted: a wild knot. Indeed, at each step, the spheres reduce in size; and at each step we add more and more crosses.
Although there are explicit and precise formulas that describe exactly the position of the spheres reflected inside, unlike mirrors, which show us a flat image on the surface, this idea allows us to imagine (and study, from the point of view of mathematics) wild knots.
Aubin Arroyo He is a researcher at the IInstitute of Mathematics of the National Autonomous University of Mexico (UNAM)
Coffee and Theorems is a section dedicated to mathematics and the environment in which it is created, coordinated by the Institute of Mathematical Sciences (ICMAT), in which researchers and members of the center describe the latest advances in this discipline, share meeting points between mathematics and other social and cultural expressions and remember those who marked their development and knew how to transform coffee into theorems. The name evokes the definition of the Hungarian mathematician Alfred Rényi: “A mathematician is a machine that transforms coffee into theorems”.
Edition and coordination: Agate A. Timón G Longoria (ICMAT).
You can follow MATTER on Facebook, Twitter and Instagramor sign up here to receive our weekly newsletter.
#rope #knotted